Regression analysis is a powerful statistical tool that can be utilized for forecasting a variable or inferring causal relationships with other independent variables. While establishing causation typically requires carefully conducted experiments, many real-world applications rely on observational data for regression analysis. This blog explores how to make reasonable inferences about causality using observational data and highlights the importance of selecting appropriate independent variables.
The Challenge of Observational Data
When working with observational data, it’s essential to acknowledge that proving causation is not always feasible. Unlike carefully controlled experiments, observational data lacks the controlled conditions necessary to establish causal relationships. We cannot directly prove causation using such data. However, with careful selection of independent variables, we can still make reasonable inferences.
Specifically, when attempting to infer a causal relationship between a treatment variable and a dependent variable, it is crucial to consider other independent variables that might influence the dependent variable or the treatment variable.
Scenarios of Independent Variables
Independent variables can impact the dependent variable in various ways, and their relationship with the treatment variable can fall into several categories:
- Uncorrelated with the Treatment Variable: The independent variable affects the dependent variable but is uncorrelated with the treatment variable.
- Correlated with the Treatment Variable by Chance: The independent variable is correlated with the treatment variable purely by chance.
- Treatment Variable Affects the Independent Variable: The treatment variable influences the independent variable.
- Independent Variable Affects the Treatment Variable: The independent variable influences the treatment variable.
- Common Cause: A common cause affects both the treatment variable and the independent variable.
Understanding these scenarios can be facilitated through a visual representation shown below. This helps illustrate how independent variables can interact with both the treatment and dependent variables.
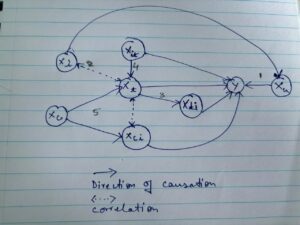
Selection of Variables
If we omit relevant independent variables from regression analysis, the treatment variable’s coefficient may capture the proxy effect of these excluded variables, thereby distorting the true causal relationship.
| Scenario | Impact of Exclusion from Regression | Impact of Inclusion on Regression | Recommendation |
| Uncorrelated | No impact on the regression coefficients Of the treatment variable | Improves the model fit by capturing variation of dependent variable explained by it. | Include in Regression |
| Correlation by chance | Distorts the actual effect of treatment variable as it picks up the proxy effect of the omitted variable | Include in Regression | |
| Common Cause | Include in Regression | ||
| Affects Treatment | Include in Regression | ||
| Treatment Affects | Exclusion will cause the treatment variable to pick up its proxy effects. | Since the treatment variable has direct effect on this, including it will cause regression model to capture variability in dependent variable through this making the treatment redundant. As a result, we may not be able gauge the effect of treatment on the dependent variable. | Exclude from Regression |
The table below summarizes the impact of extraneous independent variables on regression modelling aimed at determining the causal relationship between treatment and outcome variables.
Balancing Model Fit and Causal Inference
Inclusion of all relevant variables generally improves model fit, enhancing the accuracy of predictions or forecasts of the dependent variable. However, it is also essential to consider the potential impact on the correct causal inference of the treatment variable. A well-fitted model does not automatically guarantee accurate causal inferences, making it vital to strike a balance between model complexity and interpretability.
Conclusion
Regression analysis remains a valuable tool for both forecasting and exploring causal relationships. While observational data poses challenges for proving causation, careful selection of independent variables allows for reasonable inferences. By understanding the potential interactions between variables and including relevant factors in the analysis, we can enhance both the predictive power and the validity of our causal interpretations.
For those delving into regression analysis, it is crucial to remain mindful of these considerations to draw meaningful and accurate conclusions from your data.


